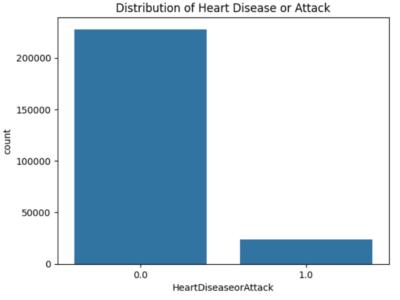
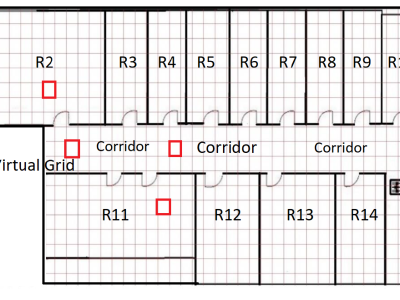
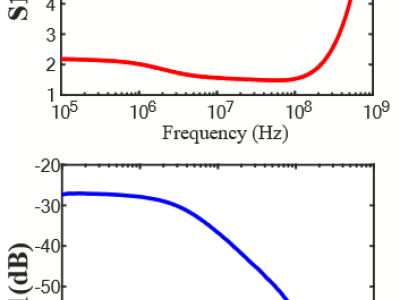
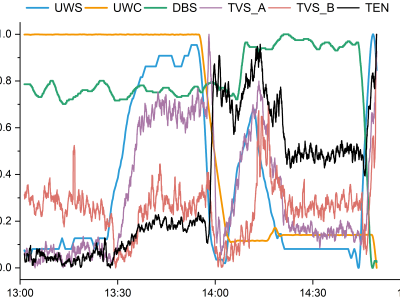
The source data files and code files of the paper: optical chaos shift keying communication system via neural network-based signal reconstruction. The following data is included:
1. Source figure file in the paper;
2. Source code of the proposed scheme, include the simulation code for communication, secure analysis and parameter mismatch range.
3. The source Simulink module is included for time-delayed chaotic signal generation.
- Categories: