Signal Processing
This dataset comprises synchronized multi-modal physiological recordings—functional Near-Infrared Spectroscopy (fNIRS), Electroencephalography (EEG), Electrocardiography (ECG), and Electromyography (EMG)—collected from 16 participants exposed to emotion-eliciting video stimuli. It includes raw signals, event markers, and Python scripts for data import and preprocessing. Special emphasis is placed on fNIRS, which, though less common in affective computing, provides valuable hemodynamic insights that complement electrical signals from EEG, ECG, and EMG.
- Categories:
98 Views
Real-time tracking of electricians in distribution rooms is essential for ensuring operational safety. Traditional GPS-based methods, however, are ineffective in such environments due to complex non-line-of-sight (NLOS) conditions caused by dense cabinets and thick walls that obstruct satellite signals. Existing solutions, such as video-based systems, are prone to inaccuracies due to NLOS effects, while wearable devices often prove inconvenient for workers.
- Categories:
20 Views
The diameter of the rivet hole is 5mm. In the experiments at the Cooperative Institute, the AE sensor spacing was set to 130mm, where the centers of sensor 1 and sensor 2 were 90mm from each end of the test piece. The waveform flow data obtained in the experiment only retained the information from 30 minutes before the crack initiation to the fracture of the test piece, and the image data of the test piece during this period were recorded.
- Categories:
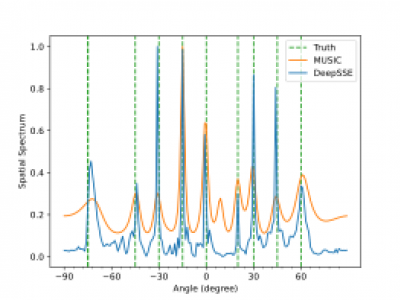
15 Views
Dataset for multiple signal DOA estmation. This the original dataset used in our research. we consider a ULA with M = 16 antenna elements spaced at half-wavelength distance (l = λ/2). We consider narrowband, non-coherent signals with different intermediate frequencies (IF) transmitted from different sources. The signals are sampled at the intermediate frequency with a sampling frequency of 2.5MHz and 300 sample points. Then we simulate the array received signal according to signal model (1) at different SNRs of {-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5} dB.
- Categories:
145 Views
This paper proposed a PE-VAE-GAN network that adaptively selected image reconstruction networks based on flow pattern classification, significantly improving the quality of Electrical Resistance Tomography (ERT) reconstructed images.To address insufficient feature extraction from voltage data,we presented a pseudo-image encoding method that converted the one-dimensional voltage signals into the two-dimensional grayscale images.
- Categories:
15 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
72 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
189 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
105 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
119 Views
At-sea testing of underwater acoustic communication systems requires resources unavailable to the wider research community, and researchers often resort to simplified channel models to test new protocols. The present dataset comprises in-situ hydrophone recordings of communications and channel probing waveforms, featuring an assortment of popular modulation formats. The waveforms were transmitted in three frequency bands (4-8 kHz, 9-14 kHz, and 24-32 kHz) during an overnight experiment in an enclosed fjord environment, and were recorded on two hydrophone receivers.
- Categories:
264 Views