Communications
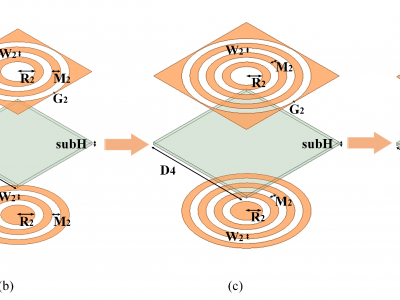
This image proposes a new class of multi-frequency band-pass frequency selective surfaces (FSSs) with ultra-high angular stability and polarization insensitivity. The proposed design consists of multiple ring slots coupled with a complementary structure on the opposite side of a single substrate layer. This approach effectively enables the design of multiband band-pass FSSs, ranging from dual-passband to penta-passband, using a simplified design process and achieving an ultra-low thickness of 0.004λ.
- Categories:
 268 Views
268 Views
The 5G network's control plane, a critical component of modern telecommunications infrastructure, manages the signaling and control functions that enable seamless connectivity and service delivery. This paper presents a comprehensive and in-depth performance evaluation of a 5G core network's control plane deployed using Open5GS and Kubernetes. The study systematically examines critical performance metrics, including latency, throughput, and resource utilization, across various load conditions, providing a nuanced understanding of the network's behavior under stress.
- Categories:
 417 Views
417 Views
Dataset containing real word data related to the informations receive on a downlink and an uplink channels. The information related to the data flowing on the channel are expressed by means of complex numbers. Some processing can be performed to convert the complex number into integer numbers in order to represent the channel as preferred. This dataset can be used to develop new compression and channel estimation algorithms.
- Categories:
 426 Views
426 Views
Test vectors are given as a part of the simulations on Gaussian noise channel. For all zero codeword transmission, a received noisy vector with length 128, the most probable L=49 messages with length 64 bit (in 16 hexadecimal), Euclidean distances and also the 64 bit indices in a 128 bit vector are provided.
- Categories:
 93 Views
93 Views
Scalability, heterogeneity, energy efficiency, cost-effectiveness, robustness, interoperability, and low latency data transfer are some of the critical challenges posed by the Internet of Things in the modern era of the Internet. Content Centric Networks (CCN) and Named Data Networks (NDN) are some proposed solutions that can meet the abovementioned challenges. In-network caching, multicasting, content security, and decoupling of data from location are the significant advantages offered by the CCN.
- Categories:
 158 Views
158 Views
Efficient and realistic tools capable of modeling radio signal propagation are an indispensable component for the effective operation of wireless communication networks. The advent of artificial intelligence (AI) has propelled the evolution of a new generation of signal modeling tools, leveraging deep learning (DL) models that learn to infer signal characteristics.
- Categories:
 1756 Views
1756 Views
Integer linear programming data on spatio-temporal degradation strategies for video rendering services in computing power networks
- Categories:
 101 Views
101 ViewsThis dataset is supplementary materials for "Study and Implementation of VLC with Angular Diversity Receiver for IoT Systems".
1. ADR Demonstraion.mp4
This describes the prototype of the ADR for IoT systems. It starts from the introduction of the prototype to the demonstration.
Real-time sensor data transmission is demonstrated. The monitor shows the light sensor value at the access point and the user node.
2. Mobile suitability Demonstration.mp4
- Categories:
 624 Views
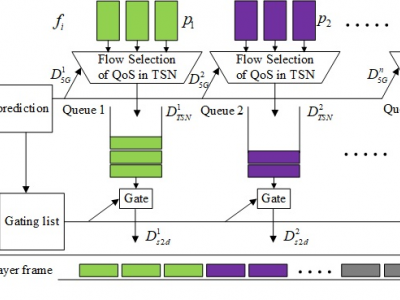
624 ViewsThis dataset includes channel delay data for 5G and TSN networks.The 5G and TSN channel delay dataset includes a training set and a test set, with 600 sets of data in the training set and 200 sets of data in the test set, which are used for channel model prediction. The data in these datasets are real, collected in real-time from the running 5G-TSN system using network testers and data packet capture tools.
- Categories:
 677 Views
677 Views