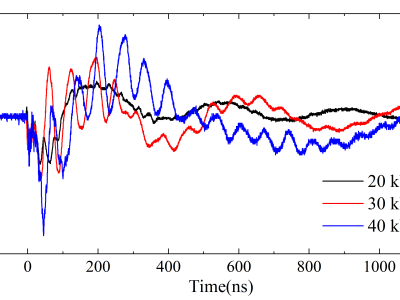
Coupled current waveforms at inverter #1 port PV+ for different field strengths.
- Categories:

Coupled current waveforms at inverter #1 port PV+ for different field strengths.

There are two main battery voltage levels (400 V and 800 V) for electric vehicles (EVs). Conventional wireless power transfer (WPT) systems utilize different connection circuits to accommodate these voltages, which may cause additional power losses. This paper proposes a new LCC-LCC WPT system to accommodate both 400 V and 800 V battery voltages without compromising performance.

As global energy shortages intensify and the drive for Sustainable Development Goals (SDGs) grows, enhancing energy efficiency in agriculture has become a pivotal factor in fostering green development. Energy Performance Contracting (EPC) presents a key opportunity for achieving energy conservation and emission reduction, but these projects are often beset by significant risks due to their complexity.

This dataset encompasses crucial power - related information. It includes network parameters, which are fundamental for grid analysis. Thermal generator parameters detail the characteristics of thermal power units. Load power data reflects consumption demands, while the wind power output upper limit defines the potential of wind energy. Dispatch results summarize the optimized power distribution, all valuable for power system research and operation.
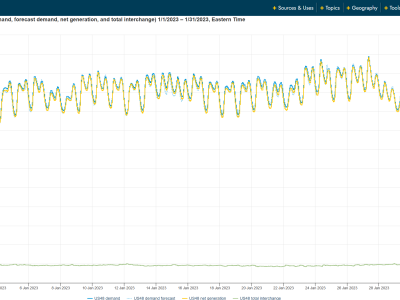
This dataset contains hourly electricity demand data and corresponding weather indicators collected from 2021 to 2023. The electricity data was sourced from the U.S. Energy Information Administration (EIA), covering both winter and summer periods across three years. Weather features—including temperature, wind speed, and humidity—were collected to capture the external conditions affecting demand. All files are stored in CSV format and aligned by timestamp. This dataset supports research in time series forecasting, demand prediction, and energy systems modeling.

Radio frequency converter (RFC) is widely used in the semiconductor manufacturing industry, which requires high power, high efficiency, and a wide power regulation range. To fulfill these demands, this paper proposes efficient modular power amplifiers (PAs), where multiple RFC modules are constructed using full-bridge class-D PAs. The constant-current output characteristics of individual modules and the system-level power delivery capability are comprehensively analyzed.

Advanced Metering Infrastructure is prone to cyber threats and Distributed Denial of Service is renowned attack that threatens critical infrastructure. Intrusion detection schemes proposed in earlier works consider the network specific parameters for intrusion detection rather than physical layer parameters. Hence, the proposal considers the physical layer parameters in detecting distributed denial of service attack through abnormal energy consumption pattern of the Data concentrator in the advanced metering infrastructure.
To evaluate the thermal behavior of multiple battery cells under operational conditions, a series of controlled temperature tests were conducted. First, each cell was equipped with calibrated thermocouples (type K) attached to its surface at the geometric center to ensure consistent temperature acquisition. The cells were then placed in a thermal chamber to maintain a constant ambient temperature. A programmable charge/discharge unit was used to apply identical current profiles to all cells simultaneously.

This dataset presents the distribution networks developed in our unpublished paper, "US Representative Feeder Sets for Distribution Grid Economics and Policy Applications." In the paper, we generate feeder sets that reproduce the economic characteristics of local distribution grids by starting from prototypical feeders that represent the electric installations in a specific location.
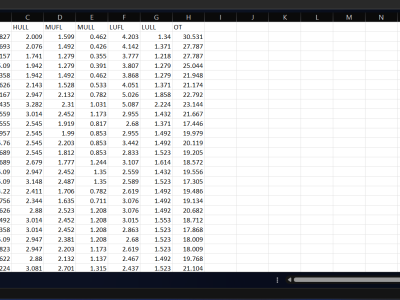
This dataset is a unified compilation of the Electricity Transformer Temperature (ETT) datasets: ETTh1, ETTh2, ETTm1, and ETTm2. It includes both hourly and minute-level temperature and load data collected from power transformers, which are vital for developing and benchmarking time-series forecasting models. The dataset contains features such as high and medium voltage transformer temperatures (HUFL, HULL, MUFL, MULL) and the operational temperature (OT), which serves as the primary prediction target.