Artificial Intelligence
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
37 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
80 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
40 Views
This dataset contains raw FMCW radar signals collected for human localization and activity monitoring in indoor environments. The data was recorded using mmWave radar sensors across two different laboratory settings, designed to simulate real-life scenarios for human detection and localization tasks.
- Categories:
46 Views
The spectrum of the Laplace-Beltrami (LB) operator is central in geometric deep learning tasks, capturing intrinsic properties of the shape of the object under consideration. The best established method for its estimation, from a triangulated mesh of the object, is based on the Finite Element Method (FEM), and computes the top k LB eigenvalues with a complexity of O(Nk), where N is the number of points.
- Categories:
86 Views
- Categories:
7 Views
https://github.com/GraphDetec/MGTAB
MGTAB is the first standardized graph-based benchmark for stance and bot detection. MGTAB contains 10,199 expert-annotated users and 7 types of relationships, ensuring high-quality annotation and diversified relations.
The components in the datasets:
- Categories:
2 Views
https://github.com/GraphDetec/MGTAB
MGTAB is the first standardized graph-based benchmark for stance and bot detection. MGTAB contains 10,199 expert-annotated users and 7 types of relationships, ensuring high-quality annotation and diversified relations.
The components in the datasets:
- Categories:
Views
https://github.com/PatriciaXiao/TIMME/tree/master/data/P_all
The components in the datasets:
- Categories:
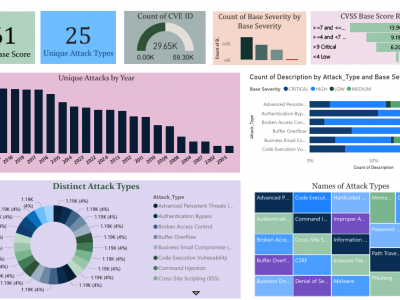
7 Views
The CyberAlert-25 Dataset is a comprehensive collection of curated cyber threat data, developed to support advanced research in vulnerability detection, classification, and threat intelligence. Aggregated from authoritative sources such as the National Critical Information Infrastructure Protection Center (NCIIPC) and the MITRE Corporation, the dataset focuses on Common Vulnerabilities and Exposures (CVEs), encompassing a total of 29,650 entries.
- Categories:
76 Views