On Balancing Phase Angles with Droop Control
- Citation Author(s):
-
Brian Johnson (University of Texas)Alejandro Domınguez-Garcia (University of Illinois)
- Submitted by:
- Siddharth Raju
- Last updated:
- DOI:
- 10.21227/y1pc-5a61
 360 views
360 views
- Categories:
- Keywords:
Abstract
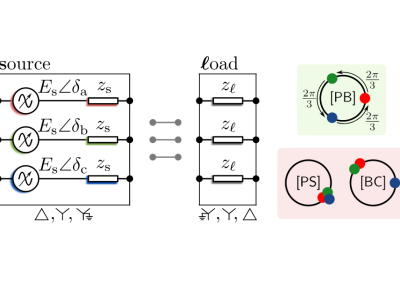
We establish topological and parametric conditions under which phase angles across three identical impedances can be balanced with small-signal stability guarantees when served from three single-phase sources executing active-power frequency droop control. All standard topologies involving Delta and Wye interconnections of sources and loads are examined. The equilibria of phase-angle dynamics are shown to include the desired phase-balanced state, but in addition, they also exhibit an undesirable phase-synchronized state and bi-cluster synchronous state (in which two of the phase angles coincide). The aforementioned analytical conditions for asymptotic stability of phase-balanced equilibria are uncovered by examining the spectral properties of the Jacobian of the linearized dynamics. Simulation results validate the analytical findings.
Instructions:
Content:
1. UnifiedClosedForm.pdf: This contains the step-by-step derivation for every expression in the paper.
2. Notebook.mlx (verified to be working on Matlab 2023a): Matlab live script file to:
- Verify all the closed-form expressions obtained for the different topologies,
- Verify the equilibrium points,
- Verify/determine the stability constraints,
- Generate the vector plot for the phase-angle dynamics.
3. TimeDomainSimulation folder (verified to be working on Matlab 2023a): Simulink model for the time-domain simulation for (Δ/Y) and (Y/Y) cases.
Instruction to run the live script:
- Requires MATLAB (tested on 2023a).
- This document is self-explanatory. Initialize all the parameters in the script, including selecting the desired topology.
- Run the script. The results will show up against each section on the right.
Instruction to run the time-domain simulation :
- Requires MATLAB Simulink (tested on 2023a).
- Run the "init.m" file to initialize all the parameters.
- Run either the "delta_y.slx" for the (Δ/Y) case or the "y_y.slx" for the (Y/Y) case.