6G and Beyond Dense Network Deployment: A Deep Reinforcement Learning Approach

- Citation Author(s):
-
Jie Zhang
- Submitted by:
- Jie Zhang
- Last updated:
- DOI:
- 10.21227/c390-dh79
 142 views
142 views
- Categories:
- Keywords:
Abstract
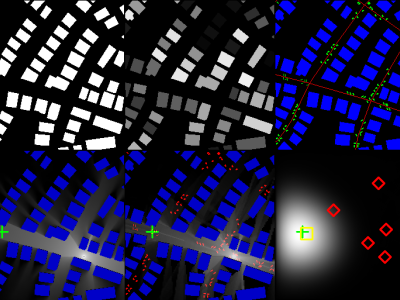
Integrated Access and Backhaul (IAB) networks
offer a versatile and scalable solution for expanding broadband
coverage in urban environments. However, optimizing the deploy-
ment of IAB nodes to ensure reliable coverage while minimizing
costs poses significant challenges, particularly given the location
constraints and the highly dynamic nature of urban settings. This
work introduces a novel Deep Reinforcement Learning (DRL)
approach for IAB network planning, considering urban con-
straints and dynamics. We employ Deep Q-Networks (DQNs) with
action elimination to learn optimal node placement strategies.
Our framework incorporates DQN, Double DQN, and Dueling
DQN architectures to handle large state and action spaces ef-
fectively. Simulations across various initial donor configurations,
including five-dice, vertical, and pentagon patterns, demonstrate
the superiority of our DRL approach. The Dueling DQN achieves
the most efficient deployment, reducing node count by an average
of 12.3% compared to a heuristic method. This study highlights
the potential of advanced DRL techniques in addressing complex
network planning challenges, offering an efficient and adaptive
solution for IAB deployment in diverse urban environments.
Instructions:
\subsubsection{Reward Function (R)}
The reward function aims to optimize the network deployment by minimizing the number of nodes and ensuring all areas are covered and all deployed nodes are connected. It is formulated as follows:
\[
\begin{aligned}\small
R(s, a, s') = & -\alpha \cdot \left( \sum_{i \in \text{Not Covered}} \text{Area}_i \right) - \beta \cdot \left( \sum_{i=1}^{n} d'_i \right) \\
& +
\begin{cases} \small
\text{when } \text{coverage\_percentage} < \text{coverage\_threshold:} \\
\left(-\frac{\text{coverage\_percentage}}{coverage\_threshold} \cdot \lambda\right) & \\
\text{when } \text{coverage\_percentage} \geq \text{coverage\_threshold:} & \\
\gamma \cdot \exp(\text{coverage\_percentage} - \text{coverage\_threshold})
\end{cases} \\
& - (\cdot \sum_{i=1}^{n} d'_i - \text{refer\_node\_count}) \cdot \text{penalty}
\end{aligned}
\]
Where:
\begin{itemize}\small
\item $\alpha$ is the penalty coefficient for the sum of the areas not covered.
\item $\beta$ is the penalty coefficient for deploying additional nodes.
\item $\text{Area}_i$ represents the area of the $i$-th grid that is not covered.
\item $d'_i$ indicates the deployment status in the new state $s'$.
\item $\lambda$ is the penalty coefficient for not achieving coverage threshold.
\item $\gamma$ is the reward coefficient for achieving coverage threshold.
\end{itemize}





Hello Jie,
This is Kian and I am a reseracher at Fujitsu Network Communications. I came across this page and I realized that you work could be very helpful in my reserach. I would highly appreciate if you could share your data with me.
Best Regards,
Kian