Validation of electromagnetic scattering from a 2D slot backed by a semielliptical cavity: Part II

We have developed exact analytical solutions of new canonical electromagnetic scattering problems. These new analytical solutions provide benchmarks for the validation of computational electromagnetic software.

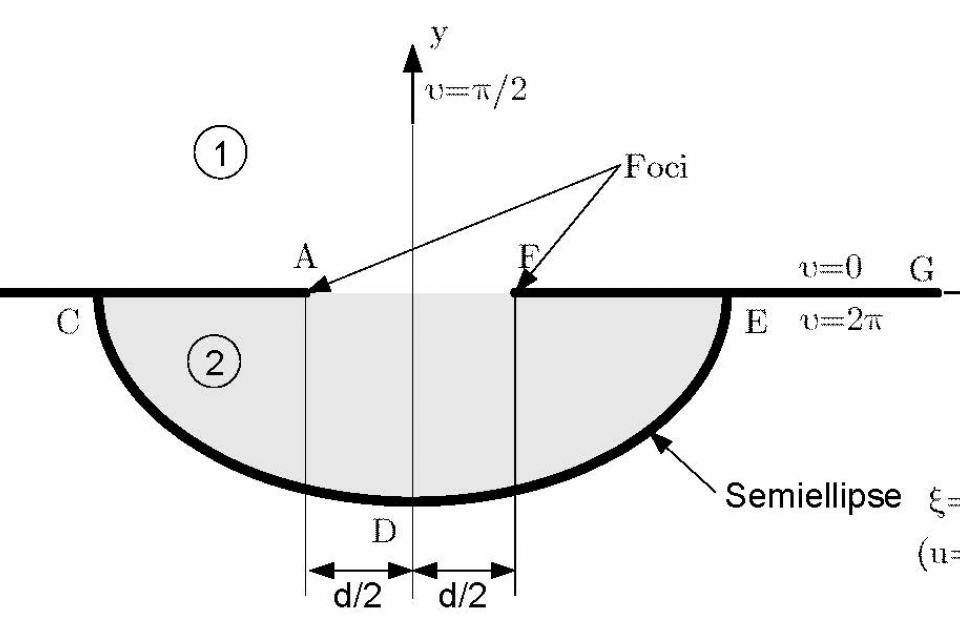
The associated article considers the electromagnetic penetration through an aperture into a cavity. The structure of interest is a semielliptical channel flush-mounted under a metal plane and slotted along the interfocal distance of its cross-section. The channel is filled with a material isorefractive to the medium that occupies the half-space above the metal plane. Three independent integral equations are developed to compute the currents induced on the structure of interest by plane wave and line source excitations. Numerical results from the integral equation methods are compared with the evaluation of the analytical expressions, derived in a previous paper, that involve the summation of Mathieu functions. Data are presented for two polarizations, various values of intrinsic impedances and ratio between aperture width and incident radiation wavelength. Further data are presented for the bistatic radar cross-section of the structure of interest. All data obtained from the integral equation methods and the evaluations of the analytical formulas are in excellent agreement.