Static and Adaptive Quantum Circuits for Co-Design and Multi-threading Partitioning Approach

Citation Author(s):
Waldemir
Cambiucci
University of Sao Paulo
Regina
Melo Silveira
University of Sao Paulo
Wilson
Vicente Ruggiero
University of Sao Paulo
Submitted by:
WALDEMIR CAMBIUCCI
Last updated:
Tue, 12/17/2024 - 09:17
DOI:
10.21227/mtr0-sp35
Data Format:
plain text
License:
Creative Commons Attribution
37 Views
Categories:
Other
Keywords:
Quantum Computing; Distributed Quantum Computing; Hypergraphic Partitioning;
0
0 ratings - Please login to submit your rating.
ACCESS DATASET CITE SHARE/EMBED

Abstract 

Quantum computing stands at the forefront of technological innovation, promising to revolutionize fields ranging from cryptography to material science by leveraging the unique properties of quantum mechanics. Central to the advancement of quantum computing is the development of efficient and scalable quantum circuits, which serve as the fundamental building blocks for quantum algorithms. Traditional static quantum circuits, while powerful, often face limitations in flexibility and efficiency, particularly as the complexity of quantum algorithms increases.

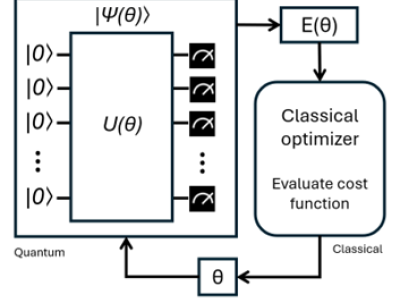
In recent years, adaptive quantum circuits have emerged as a compelling alternative to static circuits. Unlike their static counterparts, adaptive circuits possess the ability to dynamically adjust their structure and parameters in real-time based on intermediate measurement outcomes. This adaptability enhances both the flexibility and efficiency of quantum computations, enabling more responsive and optimized processing of quantum information. However, the dynamic nature of adaptive circuits introduces significant challenges in their design, optimization, and partitioning, necessitating novel approaches to effectively manage their complexity.

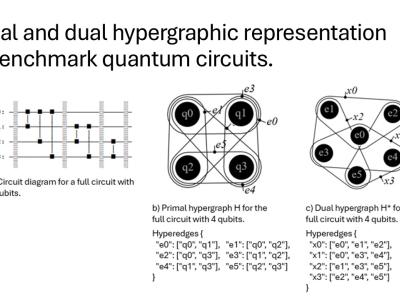
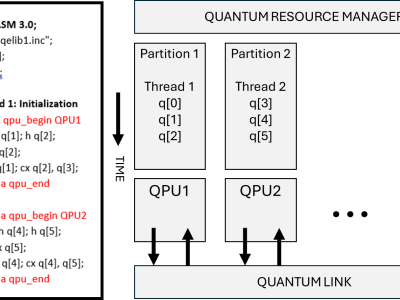
A critical aspect of optimizing quantum circuits, whether static or adaptive, is the partitioning of circuits to minimize resource usage and maximize performance. Traditional partitioning techniques often fall short when applied to adaptive circuits due to their inherent dynamism and the intricate dependencies introduced by intermediate measurements. To address this, hypergraph representations have been proposed as a robust framework for modeling adaptive quantum circuits. In this representation, groups of quantum gates are encapsulated as hyperedges, allowing for a more nuanced depiction of gate interactions and dependencies. This extended hypergraph not only captures the structural intricacies of adaptive circuits but also integrates constraints that are pivotal during the partitioning process, ensuring that groups of ports associated with classical operations are preserved.

Recognizing the need for benchmarks to evaluate and advance partitioning techniques for adaptive quantum circuits, this dataset introduces an initial set of benchmark quantum circuits. This dataset was curated to encompass a diverse array of quantum algorithms and configurations, tailored to assess both static and adaptive circuit approaches. By providing this dataset, we aim to share with the research community a valuable resource that facilitates the comparative analysis of different partitioning heuristics and optimization strategies. The availability of such standardized benchmarks is essential for driving forward the development of more efficient and effective quantum circuit methodologies.

Instructions: 

The dataset contains a collection of quantum circuit files located in several folders, for static and adaptive quantum circuits as benchmarks:

For adaptive quantum circuits, we have:

\adaptive_circuits\ipe\adaptive_ipe_16.qasm

\adaptive_circuits\ipe\adaptive_ipe_24.qasm

\adaptive_circuits\ipe\adaptive_ipe_32.qasm

\adaptive_circuits\ipe\adaptive_ipe_40.qasm

\adaptive_circuits\ipe\adaptive_ipe_48.qasm

\adaptive_circuits\qpe\adaptive_qpe_16.qasm

\adaptive_circuits\qpe\adaptive_qpe_24.qasm

\adaptive_circuits\qpe\adaptive_qpe_32.qasm

\adaptive_circuits\qpe\adaptive_qpe_40.qasm

\adaptive_circuits\qpe\adaptive_qpe_48.qasm

\adaptive_circuits\rnd\adaptive_random_16.qasm

\adaptive_circuits\rnd\adaptive_random_24.qasm

\adaptive_circuits\rnd\adaptive_random_32.qasm

\adaptive_circuits\rnd\adaptive_random_40.qasm

\adaptive_circuits\rnd\adaptive_random_48.qasm

\adaptive_circuits\rus\adaptive_rus_16.qasm

\adaptive_circuits\rus\adaptive_rus_24.qasm

\adaptive_circuits\rus\adaptive_rus_32.qasm

\adaptive_circuits\rus\adaptive_rus_40.qasm

\adaptive_circuits\rus\adaptive_rus_48.qasm

\adaptive_circuits\vqe\adaptive_vqe_ansatz_16.qasm

\adaptive_circuits\vqe\adaptive_vqe_ansatz_24.qasm

\adaptive_circuits\vqe\adaptive_vqe_ansatz_32.qasm

\adaptive_circuits\vqe\adaptive_vqe_ansatz_40.qasm

\adaptive_circuits\vqe\adaptive_vqe_ansatz_48.qasm

 

For static quantum circuits, we have:

\static_circuits\rus\static_rus_16.qasm

\static_circuits\rus\static_rus_24.qasm

\static_circuits\rus\static_rus_32.qasm

\static_circuits\rus\static_rus_40.qasm

\static_circuits\rus\static_rus_48.qasm

\static_circuits\ipe\IQPE_nativegates_ibm_qiskit_opt0_16.qasm

\static_circuits\ipe\IQPE_nativegates_ibm_qiskit_opt0_24.qasm

\static_circuits\ipe\IQPE_nativegates_ibm_qiskit_opt0_32.qasm

\static_circuits\ipe\IQPE_nativegates_ibm_qiskit_opt0_40.qasm

\static_circuits\ipe\IQPE_nativegates_ibm_qiskit_opt0_48.qasm

\static_circuits\qpe\qpeexact_nativegates_ibm_qiskit_opt0_16.qasm

\static_circuits\qpe\qpeexact_nativegates_ibm_qiskit_opt0_24.qasm

\static_circuits\qpe\qpeexact_nativegates_ibm_qiskit_opt0_32.qasm

\static_circuits\qpe\qpeexact_nativegates_ibm_qiskit_opt0_40.qasm

\static_circuits\qpe\qpeexact_nativegates_ibm_qiskit_opt0_48.qasm

\static_circuits\rnd\random_nativegates_ibm_qiskit_opt0_16.qasm

\static_circuits\rnd\random_nativegates_ibm_qiskit_opt0_24.qasm

\static_circuits\rnd\random_nativegates_ibm_qiskit_opt0_32.qasm

\static_circuits\rnd\random_nativegates_ibm_qiskit_opt0_40.qasm

\static_circuits\rnd\random_nativegates_ibm_qiskit_opt0_48.qasm

\static_circuits\vqe\vqe_nativegates_ibm_qiskit_opt0_16.qasm

\static_circuits\vqe\vqe_nativegates_ibm_qiskit_opt0_24.qasm

\static_circuits\vqe\vqe_nativegates_ibm_qiskit_opt0_32.qasm

\static_circuits\vqe\vqe_nativegates_ibm_qiskit_opt0_40.qasm

\static_circuits\vqe\vqe_nativegates_ibm_qiskit_opt0_48.qasm

We also provide in this dataset the main series of static quantum circuits created using the MQTBench tool, for static circuits in different set of configurations and levels of optimizations. A compreensive explanation about MQTBench tool we can find here:

QUETSCHLICH, Nils; BURGHOLZER, Lukas; WILLE, Robert. MQT Bench: Benchmarking software and design automation tools for quantum computing. Quantum, v. 7, p. 1062, 2023. vhttps://arxiv.org/abs/2204.13719

 

Dataset Files

LOGIN TO ACCESS DATASET FILES

 

QUESTIONS?