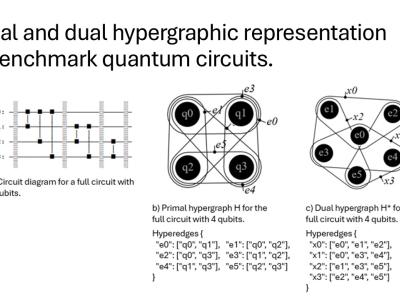
Primal and dual hypergraphic representation for quantum circuits in hypergraphic partitioning

In the context of circuit cutting and hypergraph-based partitioning, we have compiled an extensive dataset consisting of approximately 2GB of data spread across 5,000 files. These files are organized into three primary categories of experiments:

1. Full Circuits
2. Benchmark Circuits
3. Random Circuits

Each category is designed to facilitate a comprehensive exploration of circuit cutting strategies and hypergraph partitioning heuristics, incorporating considerations of both native gate sets (specific to quantum hardware) and hardware-independent (universal) gate sets.

1. Full Circuits

The Full Circuits category contains quantum circuits where every possible combination of qubits is engaged through two-qubit (binary) gates. Specifically, for a circuit with n qubits, there is exactly one two-qubit gate between every unique pair of qubits, resulting in a fully connected topology. These circuits maximize qubit interactions and entanglement, presenting significant challenges for partitioning due to their high degree of connectivity.

Characteristics:

- Number of Qubits: Varies, often scaling up to large sizes (e.g., from 4 to 120 qubits).

- Gate Sets: Includes both native gate sets and hardware-independent gate sets.

- Files Included:

• OpenQASM Files: Original circuit descriptions.
• Primal Hypergraph Representations: Qubits as vertices and gates as hyperedges.
• Dual Hypergraph Representations: Qubits as hyperedges and gates as nodes.

Purpose:

• To test the limits of hypergraph partitioning algorithms on circuits with maximal connectivity.
• To evaluate how different gate sets influence the partitioning process in fully connected circuits.
• To explore strategies for minimizing communication overhead when distributing these circuits across multiple quantum processing units (QPUs).

2. Benchmark Circuits

The Benchmark Circuits category comprises selected quantum circuits ranging from 4 to 120 qubits, derived from well-known families of quantum algorithms. These circuits serve as standard benchmarks in quantum computing research, enabling consistent evaluation of algorithm performance and hardware capabilities.

Included Algorithm Families:

• AE (Amplitude Estimation)
• Grover's Algorithm
• QAOA (Quantum Approximate Optimization Algorithm)
• QFT (Quantum Fourier Transform)
• QPE (Quantum Phase Estimation)
• VQE (Variational Quantum Eigensolver)

Characteristics:

- Gate Sets:

• Native Gate Sets: Circuits optimized for specific quantum hardware.
• Hardware-Independent Gate Sets: Universal circuits not tied to any particular hardware.

- Optimization Levels: For native gate circuits, multiple Qiskit optimization levels (OPT0, OPT1, OPT2, OPT3) are applied to assess their impact on partitioning.

- Files Included:

• OpenQASM Files: Original circuit descriptions.
• Primal Hypergraph Representations
• Dual Hypergraph Representations

Purpose:

• To evaluate the effectiveness of circuit cutting and hypergraph partitioning across various quantum algorithms.
• To analyze how different optimization levels and gate sets affect partitioning strategies and outcomes.
• To facilitate comparative studies between circuits with varying degrees of complexity and connectivity.

3. Random Circuits

The Random Circuits category includes randomly generated quantum circuits with qubit counts ranging from 4 to 120 qubits. These circuits introduce variability in gate sequences and qubit interactions, simulating a wide array of possible circuit configurations.

Characteristics:

- Gate Sets:

•   Native Gate Sets
•   Hardware-Independent Gate Sets

- Variability: Randomized gate applications and qubit interactions to mimic unpredictable circuit structures.

- Files Included:

•   OpenQASM Files
•   Primal Hypergraph Representations
•   Dual Hypergraph Representations

Purpose:

• To test the robustness and general applicability of circuit cutting heuristics under diverse and unpredictable circuit structures.
• To assess how randomness in circuit design impacts partitioning strategies and the resulting communication overhead in distributed quantum computing environments.
• To explore partitioning methods without reliance on predictable circuit patterns.

Considerations on Gate Sets

We are still exploring the impact of different gate-sets used in quantum circuits:

Native Gate Sets: Gate sets specific to particular quantum hardware, including native operations that the hardware can perform directly. Impact on Partitioning:

• Hardware constraints such as connectivity and native gate availability can affect circuit structure and, consequently, the hypergraph representation.
• Different optimization levels (OPT0 to OPT3) can significantly alter the circuit, influencing the partitioning process.

Hardware-Independent (Universal) Gate Sets: Standardized gate sets (e.g., universal gates like H, X, CNOT) that are not specific to any quantum hardware. Impact on Partitioning:

• Provides a consistent basis for evaluating partitioning heuristics without hardware-specific constraints.
• Facilitates the study of partitioning strategies based purely on algorithmic complexity and connectivity.

Optimization Levels in Qiskit

We are also exploring the impact of different optimization leves used in quantum circuits during the circuit cutting. The circuits utilizing native gate sets are provided at multiple optimization levels (OPT0-OPT3) as defined by IBM's Qiskit platform.

• OPT0 (Level 0): No optimization; minimal transformations.
• OPT1 (Level 1): Light optimization; basic gate fusion and removal of redundant gates.
• OPT2 (Level 2): Medium optimization; advanced techniques to reduce gate count and depth.
• OPT3 (Level 3): Heavy optimization; aggressive transformations that may significantly alter the circuit structure.

This dataset serves as a comprehensive resource for advancing the study of circuit cutting and hypergraph-based partitioning in quantum computing. By leveraging this dataset, which encompasses a significant volume of data across thousands of files, the quantum computing community can make meaningful progress in overcoming the limitations of Noisy Intermediate-Scale Quantum (NISQ) devices. The dataset's diversity and depth enable comprehensive studies that can inform the design of future quantum algorithms and hardware, ultimately bringing us closer to realizing the full potential of quantum computing.