Datasets
Standard Dataset
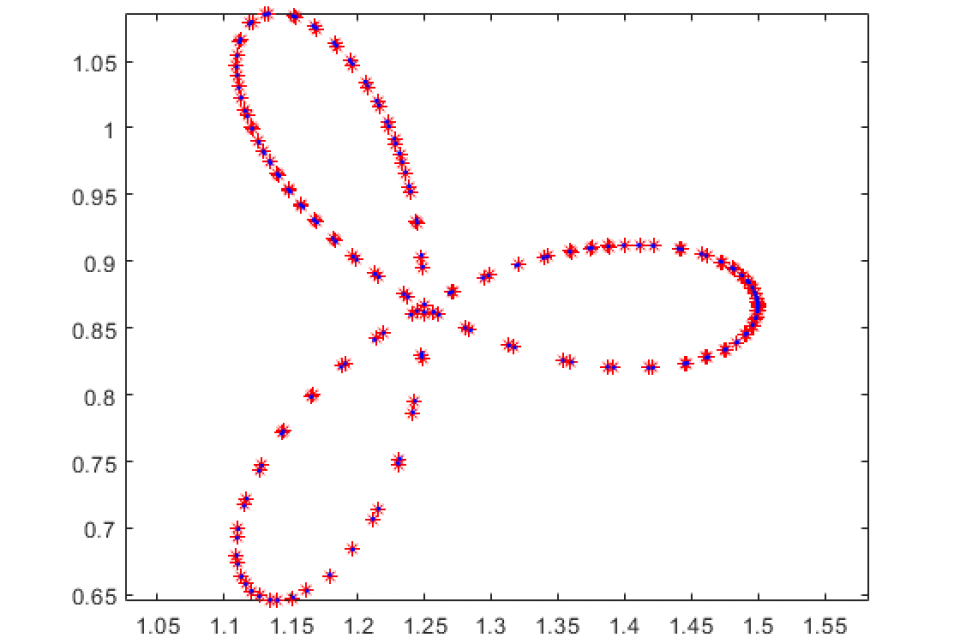
PNSND: A Novel Solution for Dynamic Nonlinear Equations and Its Application to Robotic Arm
- Citation Author(s):
- Submitted by:
- jie huang
- Last updated:
- Wed, 06/05/2024 - 07:46
- DOI:
- 10.21227/mdew-hf56
- License:
 224 Views
224 Views- Categories:
- Keywords:
Abstract
Dynamic nonlinear equations (DNEs) are essential for modeling complex systems in various fields due to their ability to capture real-world phenomena. However, the solution of DNEs presents significant challenges, especially in industrial settings where periodic noise often compromises solution fidelity. To tackle this challenge, we propose a novel approach called Periodic Noise Suppression Neural Dynamic (PNSND), which leverages the gradient descent approach and incorporates velocity compensation to overcome the limitations of the traditional Gradient Neural Dynamic (GND) model. Additionally, the PNSND model aims to suppress periodic noise by addressing its harmonic properties according to the method of Fourier decomposition of harmonics. In the paper, we explore the performance of convergence and robustness of the PNSND model. Moreover, we demonstrate the effectiveness of the PNSND model in addressing dynamic nonlinear problems under periodic noise interference through its application to robotic arm, highlighting its practical significance in industrial contexts.
<p>Compile the code to get the data</p>
Documentation
| Attachment | Size |
|---|---|
| 9.75 KB |