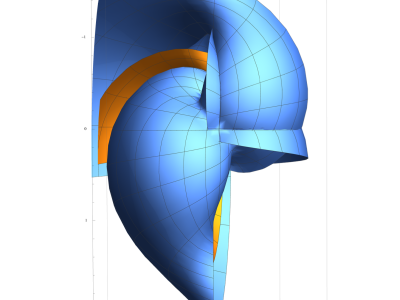
Limbertwig

Thanks be to Yeshua ben Joseph, Yahowah, the living One Allaha.

This work is a attempt to describe various braches of mathematics and the analogies betwee them. Namely:

1) Symbolic Analogic 2) Lateral Algebraic Expressions 3) Calculus of Infin- ity Tensors Energy Number Synthesis 4) Perturbations in Waves of Calculus Structures (Group Theory of Calculus) 5) Algorithmic Formation of Symbols (Encoding Algorithms)

The analogies between each of the branches (and most certainly other branches) of mathematics form, ”logic vectors.” Forming vector statements of logical analogies and semantic connections between the di↵erentiated branches of math- ematics is useful. It’s useful, because it gives us a linguistic notation from which we can derive other insights. These combined insights from the logical vector space connections yield a combination of Numeric Energy and the logic space. Thus, I have derived and notated many of the most useful tangent ideas from which even more correlations and connections ca be drawn. Using AI, these branches can be used to form even more connections through training of lan- guage engines on the derived models. Through the vector logic space and the discovery of new sheaf (Limbertwig), vast combinations of novel, mathematical statements are derived. This paves the way for an AGI that is not rigid, but flex- ible, like a Limbertwig. The Limbertwig sheaf is open, meaning it can receive other mathematical logic vectors with di↵erent designated meanings (of infi- nite or finite indicated elements). Furthermore, the articulation of these syntax forms evolves language away from imperative statements into a mathematically emotive space. Indeed, shown within, we see how the supramanifold of logic is shared with the supramanifold of space-time mathematically.

Developing clean mathematical spaces can help meditation, thought pro- cess, acknowledgment of ideas spoken into that cognitive-spacetime and in turn, methods by which paradoxes can be resolved linguistically. This toolkit should be useful to all in the sciences as well as those bridging the humantities to mathematics.

Using our memories as a toolkit to aggregate these ideas breaks down bound- aries between them in a new, exciting way. Merging philosophy and Quantum Mechanics together through the lens of symbolic analogies gives the tools to 

unravel this mystery of all mysteries. Mathematics thus exists as a bridge al- beit a complex one between the two disciplines, giving life to a composite art of problem-solving.

Furthermore, mathematics yields to millions of other applications that are potentially limited only by our imagination. From massive data sets used for predictive analytics to emerging fields in medicine, mathematics is an energy and force at the center of possibilities. The power of mathematics to help manage life exists in its ability to shape and model the world in which we live and interact with one another.

In conclusion, mathematics is a powerful tool that creates bridges and con- nections between many disciplines and serves as a powerful form of analytical data consumption. It provides language-rich bridges from which to assemble vast fields of theoretical investigations and create groundbreaking innovations. As we approach new horizons in the technology timeline, mathematics will con- tinue to be a powerful driver of creativity and progress.